生态学的目标之一是理解自然群落中的生物多样性是如何与其生产生物质的速率联系在一起的,如果它们是有联系的1-5。充分说明这之间的联系和其背后的过程发展有利于预测生态群落对于人类的干扰如改变非生物环境,引入新的物种或现有物种的减少会有何反应。然而经过40多年的研究和探讨,对于生物多样性和生态系统生产力之间的联系仍未形成广泛的、理论的解释。Grace等发表在Nature网站上的一篇文章6提出了将这些因素置于一个丰富的因果关系网络中而不是被视为孤立的往复的实体时可更好地理解他们之间的相互影响。
作者采用的数据来自Nutrient Network7,这是一个考察地球上以草为主的植物群落的全球科学合作项目。Grace和他的同事们采用一种检验假设的因果关系是否与收集到的变异系数一致的统计学方法---结构方程模型分析这些数据。这项研究从已有的文献出发,首先提出了一系列因果关系假设,这个假设网络涉及了生态系统及与之相关的外部环境。数据和模型的比对在两种水平下进行:Nutrient Network的多个草原之间或者同一草原的多次取样之间。
作者发现了一些令人兴奋的结果(Fig.1)。首先,作者发现生物质产生速率随着该位点的物种数目(其物种丰富度)的增长而增长。值得注意的是,这里的变量是物种多样性变化,而不是物种丰富度高的群落的饱和度。其次,不论是位点间还是位点内,较多的地面上累积的生物质(获得植物组织和死亡的物质)会减少物种丰富度。作者认为这证明了物种之间的竞争是决定群落物种丰富度的重要因素,这种竞争,至少在较小的空间尺度上,主要为光线竞争。值得注意的是,与之前认为竞争对于群落的结构影响随着生产物的增加而增强不同,不论群落的生产性如何竞争都是不可忽略的1,5。最后,这项分析确定了几条通过非生物环境(包括温度、降水、土壤性质和主要的人为干扰历史)调节生态环境中物种多样性和生产力相互作用的途径。
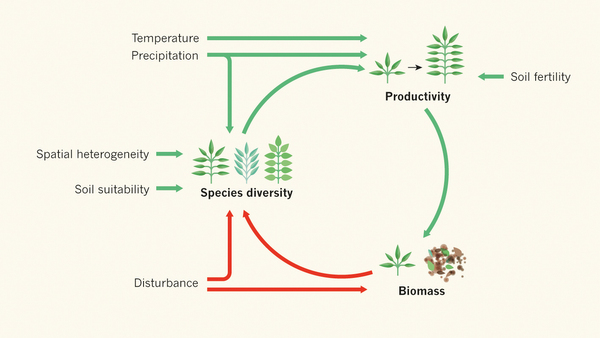
Fig.1 生物多样性和生物质产生的网络示意图。采用结构方程模型和跨越五大洲的39个草本植物群落的数据,Grace等6将生物多样性的变化和生物质的产生用因果关系网很好的阐述出来。正向途径(绿色)具有增强效果,如土壤肥力增加植物生产力;负向途径(红色)为地表上生物质(活的植物,和死亡物质)对物种多样性有抑制作用。所示的网络表示模式与39个群落之间的变化一致;群落内的变化支持比较网络。
草本植物群落提供我们知道的大部分关于生物多样性和生产力之间关系的经验1-3,5,主要是因为这些系统中的这两种实体容易被定量(当然,相对而言)。但是,自然有人会问,Grace等人设想的因果网络如何应用于其他主要生物群落,如热带雨林、珊瑚礁或人体内的微生物。因此,将作者的因果网络和物种共存和群落动态的数学理论整合,将有助于描绘网络的生物普遍性。
并且,尽管结构方程模型可以揭示数据是否与因果网一致,可能其它的关系网络与数据一致9。作者证明了他们假设的因果网络的广泛性,但是这篇文献的肯定有其他解读。其它与这些或参照数据一致的似是而非的生态学的因果网络是否可以构建是一个未解决并且需要解决的问题。
或许Grace和他的同事们最令人兴奋的贡献是他们有力地揭示了生态学理论、实验和统计实践已充分成熟,能建立一个更加整体的、系统水平视角的生产力和生物多样性的关系。这挑战了几十年的老观点,生物多样性-生产力关系可被表征为简单但普遍的二项曲线1,5。尽管普遍认为这种二项模型的预测能力很弱,且存在关于这类曲线基本形状的分歧,但仍被广泛使用1-3,5。二项模型逐渐显露的不足激发了多种可替代的更加精细的模型来描述生物多样性和生产力如何相互影响4,10,11。至此,Grace等已经完成了一个与全球各地收集起来的数据深度融合的框架。
不过,二元关系经久不衰也证明了它对处理复杂生态系统有吸引力。最终,生态学家们将会寻求预测能力与忠实于数据的平衡的概念框架。Grace等人的努力为严格审查和评估更精确生态群落的概念模型奠定了基础。随着时间的推移,这些模型或许会与多样性-生产力二元模型并驾齐驱,成为生态学思考和研究的基石,甚至有可能取代二元模型。
Kevin Gross,美国,北卡罗来纳州27695,罗利市,北卡罗莱纳州立大学,生物数学组
1. Grime, J. P. Nature 242, 344–347 (1973).
2. Mittelbach, G. G. et al. Ecology 82, 2381–2396 (2001).
3. Adler, P. B. et al. Science 333, 1750–1753 (2011).
4. Willig, M. R. Science 333, 1709–1710 (2011).
5. Fraser, L. H. et al. Science 349, 302–305 (2015).
6. Grace, J. B. et al. Nature http://dx.doi.org/10.138/ nature16524 (2016).
7. Borer, E. T. et al. Methods Ecol.Evol. 5, 65–73 (2014).
8. Cardinale, B. J. et al. Nature 486, 59–67 (2012).
9. Kline, R. B. Principles andPractice of Structural Equation Modeling 4thedn (Guilford, 2015).
10. Schmid, B. Trends Ecol. Evol. 17, 113–114 (2002).
11. Cardinale, B. J., Bennett, D. M., Nelson, C. E. & Gross,K. Ecology90, 1227–1241 (2009).
翻译:薛夏琳 审稿:冯薇
原文链接:http://www.nature.com/nature/jou ... re16867.html#access


















留言