导语:虽然纳什在博弈论上的工作更为大众所知晓, 但数学界一致认为纳什的主要贡献在几何学上。他的嵌入定理是如此美妙并具有原创性, 虽然在下文中不可能详细地解释, 但我们会看到嵌入定理有许多有意思的结果。
关键词:微分几何, 等距嵌入

上图这样的表面能被描述出来全靠纳什的工作成果。图片来源:Hevea Project, CC BY-SA
正如已被广泛报道的消息所言, 约翰·福布斯·小纳什(John Forbes Nash Jr)在今年5月23日的一场车祸中悲剧性地去世了。有许多人悼念这位伟大数学家。由于Sylvia Nasar写的纳什的传记《美丽心灵》以及接下来基于此书的电影,纳什变得有名。
纳什在博弈论上的工作被谈论得很多。但他其它的数学成就较少被谈及。我认为,许多理解纳什工作的数学家会认同尽管他在博弈论上的工作对其它领域的影响最大, 他还做出了其它更了不起的突破。除了博弈论之外, 纳什工作的领域还包含代数几何, 拓扑学, 偏微分方程和密码学。
但可能纳什最惊人的研究结果在几何学中。为了纪念纳什的一生, 我会试着让读者能了解一点纳什的这项工作。
约翰·纳什与纯数学
纳什的许多工作是在几何学领域的。但这种几何——微分几何, 是非常不同于我们中学学的几何学的。它不是像在中学数学课本中有关三角学和毕达哥拉斯的内容。它是有关曲面, 曲率, 光滑性这样的主题的。
像所有纯数学家一样, 纳什证明定理:严密, 恰当, 绝对正确,没有含混其辞的逻辑表述。纯数学的世界是朴素并且深奥的, 但它对真理的要求是永恒和绝对的。
很好, 那至少是理论。纯数学的突破通常在人类理解力的极限上。甚至对那些领域里的人来说也需要时间来充分理解新的进展。
纳什的工作是个很极端的例子。他的文章可以表达混乱, 很难理解,而且他对问题的处理通常与之前的的处理方法不同,。这让学生和其他的专家感到迷惑。但他在创造力上几乎是超凡脱俗的。
尽管数学上的论证是被逻辑的严密要求牢固地限制住的, 纳什在构思和方法是狂野的。而且他在几何上的工作更是如此。
纳什的几何学
取一张平整的纸。你可以弯曲它, 但不能撕扯它或弄皱它, 你能做出什么样的形状?你不能做出一个球面, 或甚至是球面的一部分。因为球面是弯曲的,但纸面是平的。
但你可以做出一个柱面。并且甚至做出一个锥面, 如果你见过傻瓜帽的话你会知道。(这个事实对于做冰激凌蛋卷来说是有用的, 见下图。)

冰激凌蛋卷的制作从一张蛋卷皮开始。图片来源:Gotham3/ingur
事实证明, 尽管柱面或锥面看上去是弯曲的, 它内蕴上是平坦的。在本科微分几何课程中(比如我在Monash上的一门课), 当我们研究这个内蕴曲率就会发现有许多平坦的曲面。
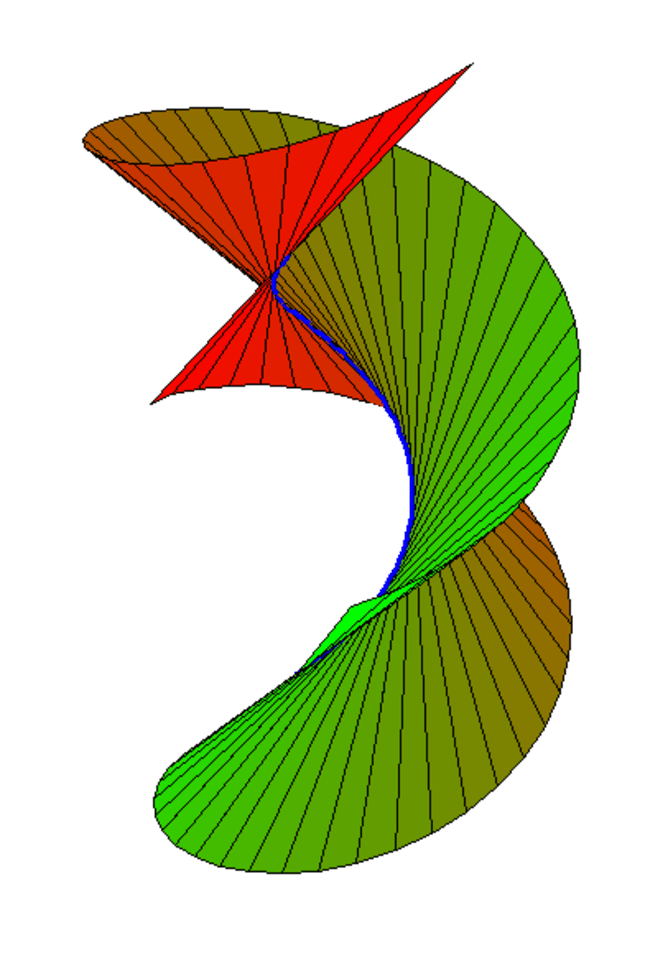
此表面尽管看上去不平,但其实是一个平面。图片来源:Richard Morris/Wikipedia
这些想法在纳什之前已存在了几百年, 但纳什把它们进一步发展了。
嵌入问题
纳什采用了"嵌入"一个曲面的想法:在不撕扯、弄皱, 或与自身交叉的情况下把它放到空间中。一个不破坏曲面内蕴几何的嵌入是“等距”的。换句话说, 上述曲面是平面到3维空间的“等距嵌入”。
我们不只可以对平面提出等距嵌入问题, 还能对任意曲面:球面, 甜甜圈(数学家称之为环面这样听起来体面一些)提出。
事实表明存在一些严重弯曲或与自身缠绕在一起的曲面不能被嵌入3维空间。事实上, 它们甚至不能被嵌入4维空间。
但纳什指出任意曲面可以被嵌入17维空间。额外的维度不但没有把问题变得更难, 实际上把问题变简单了——它给你更多地方来嵌入你的曲面!接下来, 纳什的工作被其他人完善了,我们现在知道任意曲面可以被嵌到5维空间中。
然而, 曲面是只有2维的。但纳什感兴趣的是任意维度的曲面。这些曲面的高维类比被称为“流形”。
纳什证明在不破坏流形几何的前提下, 你永远可以把它嵌入某些维度的空间中去。有了这个重大结果, 纳什解决了等距嵌入问题。
纳什的等距嵌入问题的证明对数学界的多数人来说是个完全的意外。他的方法是革命性的。大数学家米哈伊尔·格罗莫夫(Mikhail Gromov)说纳什在嵌入问题的工作震惊了他, "其难以置信的程度就像某人用头发把自己提起来那样”。但在极大的努力后, 格罗莫夫最终理解了纳什的证明。在在明白了纳什冗长的论述后, 格罗莫夫说:纳什”的确奇迹般地用头发把你提到了半空中”!
发展中的等距嵌入
受到纳什工作的启发, 格罗莫夫接着发展了自己的想法。他写了本书。此书和纳什的文章一样以其晦涩难懂在数学家中闻名。他在书中发展了一种称为“凸积分”(convex integration)的方法。
格罗莫夫的方法有几个优点。其中一个就是用凸积分的方法更容易画一个嵌入的图像。在格罗莫夫之前, 我们知道等距嵌入是存在的并具有很好的性质, 但要让它们图像化是非常困难的。这有几个原因,不只是因为它们通常的维度更高。
在2012年, 一个法国数学家团队用格罗莫夫的凸积分方法得到了等距嵌入的电脑图像。它们极度地错综复杂, 几乎类似分形, 却是光滑的。一些图像如下所示。
一粒沙中的世界
纳什在等距嵌入问题上的很多方面都有研究并引出许多后续的研究。
一个特别神奇的方面是等距嵌入是如何构造的。纳什的工作与Nicolaas Kuiper接下来的工作指出如果你想把一个曲面等距嵌入一个3维空间,只需收缩便可。
如果你有一个曲面的“收缩”嵌入,即所有长度都被缩短, 纳什和Kuiper的工作可以让你通过略微调整曲面的收缩来得到曲面的等距嵌入。
这听上去很不可思议。比如试想把一个网球的表面的半径收缩纳米级。纳什和Kuiper指出通过充分地“弄皱”曲面(但是是光滑的;没有折叠或撕扯!), 你可以在这个纳米级半径里得到一个原始网球的等距拷贝。这种“弄皱”曲面的类型被法国团队的电脑图像重现了出来。
此法国团队是这样认为的。取一张平整的方形纸片,把顶部和底部粘在一起, 会得到一个柱面。现在再把左边和右边粘在一起,你可能会发现你得到了一个甜甜圈。但你会发现纸面被褶皱或扭曲了。
你可以在不扭曲它的情况下将它嵌入3维空间吗?纳什和Kuiper说“是的”。格罗莫夫说“使用凸积分”。法国数学家说“这是它看起来的样子”!

把正方形的平面圆环嵌入周围空间。图片来源:Hevea Project, CC BY-SA
在其项目的网站上可以看到更多图片。
但此数学定理不仅适用于网球或甜甜圈:它对任意维的任意流形都成立。任何世界都能被包含在一粒沙子中。
他是如何做到的?
纳什拥有少见的天才与勤奋的结合。在SlyviaNasar所著的纳什的传记中, 她详细描述了纳什在解决问题上付出的可畏的努力和精力。
正如从电影中众所周知的那样,由于纳什患上了精神分裂症, 他开始相信包括外星人和超自然生物的奇怪的阴谋论。当后来被问到为什么他这样一个极为聪明的科学家会相信这样的事情时, 他说这些想法“出现在我头脑的方式和数学想法是一样的, 所以我认真地对待它们”。
坦白地说, 如果我的头脑能告诉我和需要证明等距嵌入定理一样准确而深刻的想法的话 ,我也会愿意相信外星人和超自然的。
(翻译:徐兆杰;审稿:傅斓)
原文链接:
https://theconversation.com/every-world-in-a-grain-of-sand-john-nashs-astonishing-geometry-42401


















留言