这是随机输入的二维威尔逊-考恩模型的数值模拟的快照。黄色（蓝色）像素代表高（低）活性。（图片来源：Tiberi等）
过去的神经科学研究表明，大脑中的生物神经网络可以自我组织到临界状态。在物理学中，临界状态本质上是物质有序相和无序相之间的过渡点。
于利希研究中心（Jülich Research Centre）、亚琛工业大学（RWTH Aachen University）和索邦大学（Sorbonne Université）的研究人员最近引入了一种可以帮助解释大脑临界状态的理论。这一理论发表在《物理评论快报》（Physical Review Letters）上的一篇论文中，基于一种典型的神经场理论，即随机的威尔逊-考恩模型（Wilson-Cowan model）。
“之前的研究提供了大脑在临界点运行的证据。”进行这项研究的Lorenzo Tiberi、Jonas Stapmanns、Tobias Kühn、Thomas Luu、David Dahmen和Moritz Helias通过邮件告诉物理学家组织网，“然而，目前尚不清楚在许多可能的临界状态中，哪一种是由大脑具体实现的，以及大脑如何利用临界状态进行最佳计算。”
为了对不同类型的临界状态进行分类，物理学家通常使用所谓的重整化群（RG）中的方法。这些本质上都是形式化的方法，可以用来系统地研究物理系统在不同尺度上的变化。
在他们的研究中，研究人员采用了这些传统方法，并将其与威尔逊和考恩首次提出的神经元场模型原型相结合。然后，他们将其应用于神经科学领域，以研究生物神经网络的临界性。
“在这项工作中，我们研究了具有随机输入的成熟的威尔逊-考恩模型，因此我们使用的模型并不新鲜。”Tiberi、Stapmanns和他们的同事说，“然而，通过使用重整化群技术，我们得到了一个原创的结果。”
为了完成计算任务，即涉及计算的认知任务，人脑需要能够记住它接收到的输入数据，然后以复杂的方式将其组合起来。这反过来又允许它处理信息并解决计算问题。
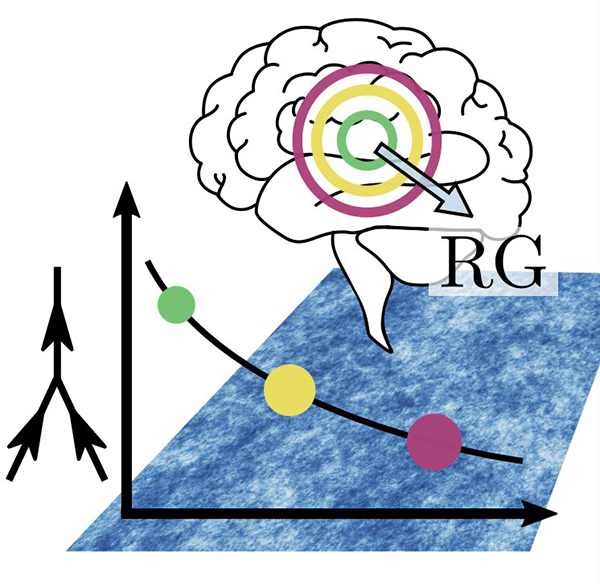
说明重整化群（RG）方法的抽象图。当在越来越粗的长度尺度上观察系统时（由同心圆和大脑前方的箭头表示），非线性相互作用的强度（由左边的费曼图表示）只会缓慢下降，特别是在大的空间尺度上仍然与零不同（带彩色点的曲线）。（图片来源：Tiberi等）
“我们发现，威尔逊-考恩神经场模型中的临界值属于Gell-Mann-Low类型，在所有临界值类型中，它特别提供了记忆输入数据和以复杂方式组合数据之间的最佳平衡。”Tiberi、Stapmanns和他们的同事说。
研究人员通过重整化群的方法研究了威尔逊-考恩模型中非线性相互作用的影响，这对于理解大脑如何处理信息至关重要。这是一项了不起的成就，因为过去其他团队使用的平均场方法无法捕捉这些影响，尤其是当交互作用强大到足以在宏观尺度上塑造大脑动力学时。
“我们希望重整化群方法将用于研究神经网络中的其他非线性过程。”该团队解释道，“此外，我们还将其与物理学的其他领域联系起来：Gell-Man低临界性的概念源于量子场论，而与我们的模型密切相关的Kardar-Parisi-Zhang模型最初用于描述界面的动态增长。”
未来，这组研究人员引入的理论可以用来研究各种其他的大脑动力学和神经过程，超越临界状态。此外，它可能最终为引入其他融合物理学和神经科学的理论结构铺平道路。
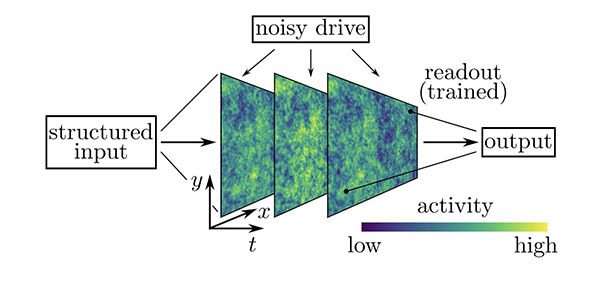
说明该模型的计算能力的调查。一个刺激（结构化输入）被添加到系统中（具有空间坐标x和y），它随着时间t而演变，同时网络也由随机输入（噪声驱动）驱动。线性读出器被训练成根据系统活动的快照来重建或分类输入刺激。重构任务测试系统的记忆能力，而分类任务则需要非线性的相互作用。（图片来源：Tiberi等）
“在大脑中，神经元之间的连接强度是高度可变的，在一级近似下，它可以被描述为随机的。”研究人员补充道，“我们现在计划将我们的方法应用于包含此功能的神经模型，看看这对我们发现的临界类型有什么影响。”
作者：Ingrid Fadelli
翻译：赵书轩
审校：张和持
引进来源：物理学家组织网
本文来自：中国数字科技馆
本文是中国数字科技馆(www.cdstm.cn)原创内容，转载请注明出处和作者，否则我们将依法追究侵权责任。
[责任编辑：环球科学]
京公网安备11010502039775号
