数学可以帮助我们绘画现实中的物体。自然界中图案的规律性能够引导艺术家们用数学概念进行艺术创作。许多植物都拥有让人惊叹的美丽枝叶，而在这其中我们可以发现一些数学模型的存在。例如，多叶芦荟（Aloe polyphylla）是生长在莱索托（非洲国家）的一种植物，它们拥有着美丽的螺旋形叶子。
用数学概念构建叶子形状的方法有很多种。一个有名的例子就是巴恩斯利市（Barnsley）的蕨类。生于1946年的著名英国数学家迈克尔·巴恩斯利（Michael Barnsley）在他名为《无处不在的分形》的书中描述了这种美丽的分形结构。他用迭代函数系统的方法创造了这种分形，且其与蕨类植物的叶形十分相似。
你可能会认为下图所示的这些叶子是手绘的，但其实它们是由计算机产生的数学图案。这些形状是用三角函数的正弦和余弦构成的。在这里，我想特别说一下我过去创作这些绘画的方法。
当我想画一个现实物体的时候，我会试着一步一步地找到一个数学公式来进行我的绘画。在每一步中，我都会在函数上增加数学表达式，以此来提升绘画与物体的相似度。通常来讲，我都会去寻找有关正弦和余弦的公式，因为这两个公式的特点（尤其是周期性，有界性和平滑性）会让它们在绘画过程中显得十分有用。然而我还是要在每一步中都找到一个合适的数学表达式，因此有些步骤会显得非常的难，甚至不可能完成。举个例子，在上图中，你可以看到一个类似日本枫叶形状的数学曲线的产生过程。图像显示的就是如何把一个圆变为一个枫叶这样的图形。
下面这些图片展示了三种用上述方法制作的数学图像，我们可以用参数方程来表示它们：
枫树叶
鸡爪槭叶
橡树叶
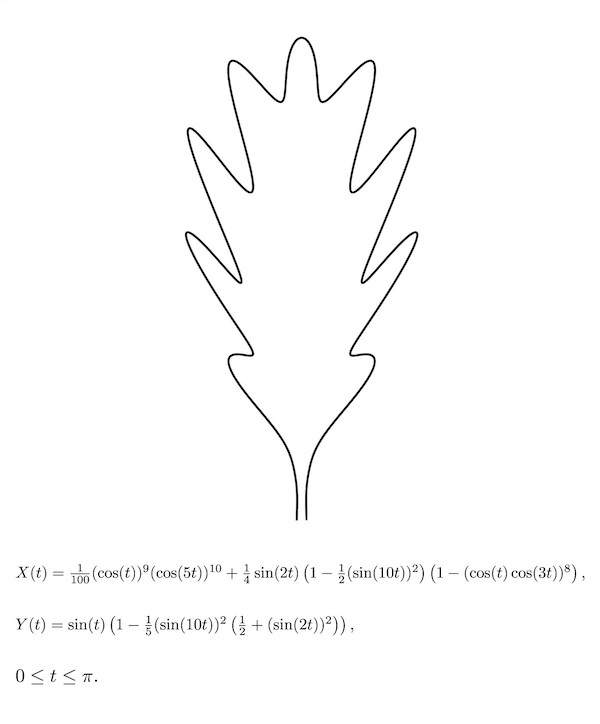
同样，在下面你可以看到通过绘制上千个圆圈所产生的数学图案。这些圆圈的半径和圆心都是由三角函数确定的。
橄榄树枝：
棕榈树枝：
作者简介：Hamid Naderi Yeganeh（哈米德·纳德利·耶根）
（翻译：孙宇辰 审校：刘财兴）
京公网安备11010502039775号
