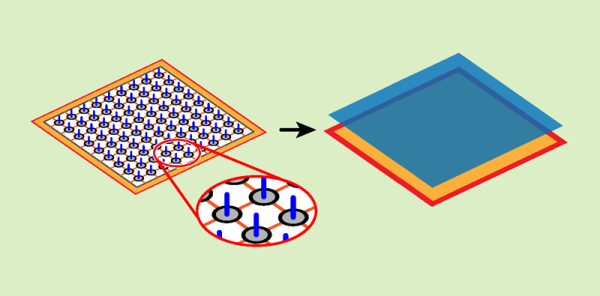
将张量网络的应用从二维网格(左)拓展到连续情形(右)。(图片来源:APS/Alan Stonebraker)
在量子力学诞生之后不久,Paul Dirac和其他人假设,原则上,量子力学可以预测一切人们想要的物体的性质。也就是说,只要我们能解出相关的量子方程。但通常情况下,这些方程极其困难,或者无法解决,就这一点来说,例如强关联电子系统和其他多体相互作用发挥重要作用的系统。解决这类多体问题将帮助我们找到新的高温超导体,设计量子计算结构,描述新奇相变。所谓张量网络,这种几十年前引入的数学工具在简化处理复杂量子系统上取得了广泛的成功。但是,到目前为止,这些工具只能用离散的方式解决空间维度高于一维的量子系统,也就是利用离散网格来表示。这样的表现形式不足以解决大量的多体问题。现在,德国马克斯普朗克量子光学研究所(Max Planck Institute for Quantum Optics in Germany)的Antoine Tilloy和Ignacio Cirac拓展了张量网络,这样他们能在任意空间维度(包括二维和三维)中展现连续系统。这个结果将帮助研究人员将张量网络应用于量子场论中的一大类问题。
在很长一段时间里,人们一直认为量子力学方程所需的计算量远远超过任何的计算机的计算能力。这是由于“维度的诅咒”:利用经典计算机模拟一个量子系统所需的参数个数似乎和系统所含的粒子数量成指数关系。费曼曾说,量子系统本身就可以成为计算源:一个量子计算机可以模拟量子系统,而不会像经典计算机一样,运行速度呈指数递减。但要建造一个能比经典计算机运行更快的量子计算机是一个挑战。但是可能还有其他方法规避指数关系,例如通过简化量子问题。张量网络提供了一个前景明朗的方法——这种优雅的数学方法已经解决了许多重要的量子系统模型。
张量网络通过由初等张量相互连接组成的网络来表示量子系统的波函数,从而提供了对量子系统的简化描述。每个张量都由一个通过导线相互连接的形状所表示(正方形、椭圆形或三角形)。经过广泛的研究确定,这些网络提供了相关量子属性的高精度编码,包括量子纠缠。重要的是,张量网络伴随着图形语言——很像著名的费曼图——能通过可视直觉来指导使用。
这种计算的优点来自张量网络以简单的结构来近似一个复杂的量子态。本质上来说,张量网络可以被认为是一种数据压缩协议,只保留了量子态那些足以描述其行为的性质。这种压缩可以极大地降低随系统规模增长的计算复杂性。利用这一优点,研究人员开发了基于张量网络的强大数值方法,如描述一维强相关系统的矩阵积态(matrix product states)和投影纠缠对态(projected entangled-pair states),以及广泛应用于二维的多尺度假定纠缠重正交化(the multiscale entanglement renormalization ansatz)。
要应用以上所提到的方法,量子系统就要被重新以初等张量的离散网格形式来表示。这是由局部自旋排列组合而成的系统的理想表示,像用于描述磁相互作用的伊辛模型(Ising models)的一维和二维自旋网格。对于其他的量子系统,强加可能不需要的晶格对称,可能会导致错误。。因此,将张量网络推广到连续的情形是一个挑战。2010年,Frank Verstraete和Cirac取得进展,他们将一维矩阵积状态扩展到连续极限,通过使晶格间距趋于零,同时重新调整张量。二者表明,扩展形式可以普遍应用于量子场论,表明它可以确定一维系统的基态。
Tilloy和Cirac现在进一步将连续的张量网络拓展到更高的维度。考虑到二维或三维的玻色子量子场(bosonic quantum fields),它们显示出的一类连续张量网络状态可以被看作离散张量网络表示的极限(图1)。这种状态有两个等价的表示,作为函数积分或作为运算符。作者证明了这些状态可以作为“一种假设”,并从中可以通过变分法计算得到n粒子波函数和相关函数的表达式。
重要的是,他们表明张量网络的连续扩展保持了一些特性,使离散张量网络成为有用的数值和分析工具。具体来说,它们具有相同的“表现形式”——在不改变系统状态的规范转换下,能够近似系统的任何状态并满足相同的不变性。
更进一步的研究需要解答一些未决之题。比如说,作者展现了只有在连续张量网络能用高斯基(Gaussian basis)表示时,系统的相关函数才能精确推导出来。这是有限的一类状态,解析解早已求出。这个方法需要推广到非高斯的情形。理解连续张量网络状态是否与它们的离散对应态类似,也服从所谓的面积定律,系统纠缠的一个基本尺度,这也是一个有趣的问题。
关于张量网络状态的这种新的连续延伸是否会导致新的物理发现,目前还没有定论。但是,人们当然希望它能提供一系列适用于处理连续系统的分析方法(例如精确的高斯函数积分、鞍点近似或图解展开)。理论工作者的方法为利用张量网络技术进一步研究量子场论奠定了基础。
这项研究发表在《物理学评论X》上。
作者:Anastasiia A. Pervishko(斯科尔科沃科学技术学院深量子实验室);Jacob Biamonte(斯科尔科沃科学技术学院深量子实验室)
翻译:王麟涛
审校:郝豪
引进来源:美国物理学会
















 京公网安备11010502039775号
京公网安备11010502039775号





