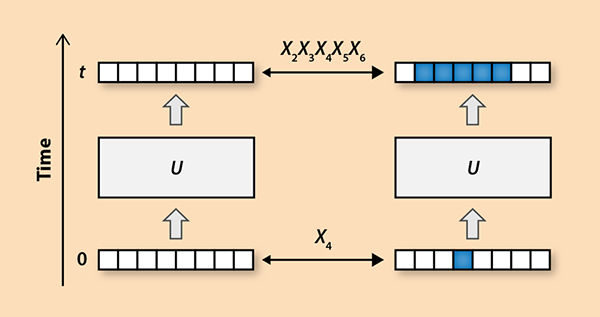
图1. “算符置乱(operator scrambling)”概念图解。在一个混沌系统中,一个在时间为0时翻转一个量子比特的算符会随着时间演化成一个翻转更多量子比特的更加复杂的算符。
在日常生活中,“混沌”描述的是一切混乱的事物。在物理学中,这个词有一个更具体的含义:它指一个即使遵从确定性规律,却由于对初始条件的指数敏感性而完全不可预测的系统——就像是蝴蝶扇动翅膀然后造成了远处的一场龙卷风。但是在经典的宏观世界中所观察到的混沌又是如何从量子力学理论所主导的微观世界中浮现出来的呢?一个最近提出的解释援引了量子“信息置乱(information scrambling)”这一算法,在这个算法中信息会被快速的分散到系统中具有量子关联的粒子中去。这种置乱是一种会造成混沌的不可预测性的失忆机制,然而发展一种可以完全描述信息置乱的理论仍然是一个艰巨的任务。现在,马里兰大学帕克分校的Shenglong Xu和Brian Swingle通过量子的布朗运动模型来研究混沌,向实现这种描述更近了一步。这一模型用量子力学算符来描述混沌,随着时间这些算符会变得越来越复杂。Xu和Swingle展示了这种形式可以实现对混沌如何在多体系统中传播的量化描述。
在经典物理中,混沌的一个常见例子是三体问题:对于两个行星围绕一个恒星运动的系统,其动向对于天体的初始位置和动量极为的敏感。初始条件与未来的位置和动量有着决定性的关联,但是这种关联会随着时间在数学上越来越复杂。
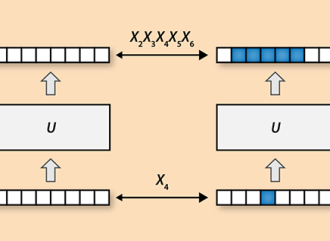
那么我们自然会问量子世界中是否存在与混沌对应的事物。在量子力学中,像是位置和动量这样的物理可观察量,由于海森堡测不准原理,成为了不能被同时以任意精度观测的算符。但是,因为初始的算符决定之后的算符,量子力学中的动力学过程还是可确定的。例如,假设处于两个态的N量子比特的系统,这两个态之间只有一个比特差别(图1),即可以用一个翻转了第四个比特的简单的算符X?将两个态联系在一起。随着时间演化,这两个态会变得十分不同,只有翻转更多的量子比特才能将它们联系起来,这意味着算符X?随着时间演变成了一个翻转更多量子比特的复杂算符。近期的研究探索了这种“算符置乱”是如何与量子混沌相关联的。
这些研究也指示了量子混沌的一些特性。在一个量子比特系统(比如一个晶体中旋转的电子们)中,在一个混沌系统中翻转一个量子比特(或者一些量子比特)就好比是在海中央引发了一场小范围的地震,最初震动只会影响到局部的海浪,但是最终它的影响可以导致一场大海啸,它的传播是由一个非线性等式所描述的。关于波前的描述——比如它的速度和形状——可以揭示掌控着波线性或非线性传播的重要信息。类似的行为也预期会出现在量子算符的动力学中(图2)。特殊的算符,如单自旋(single-spin)翻转算符,有明确的“载体(support)”——即这些算符所作用于的一组量子比特,但是当算符随时间演化,它们有可能会变成作用于多个量子比特的单自旋翻转算符的线性叠加。因此它们的载体会被定义为一个光滑的分布——就像是水波的光滑波前一样——而混沌动力学会改变这个波前的形状。Xu和Swingle的研究的一个主要目标就是为这种动力学过程提供一种量化描述。
研究算符置乱是一个艰难的任务,因为混沌系统很难用解析方法和数值方法来处理。这项研究背后的主要想法是通过引入随机性来简化这个问题。这种方法的优势在热力学中有所体现:当不可能描述一个房间内的气体分子的确切状态时,我们可以通过假设一个粒子的态的随机分布来高精度预测气体压力和温度之间的关系。然而将这种方法扩展到算符置乱中总体来说还很难,由于过去的信息会对未来有复杂的影响,即使只是确定在短时间后一个算符的尺度改变了多少都很困难。
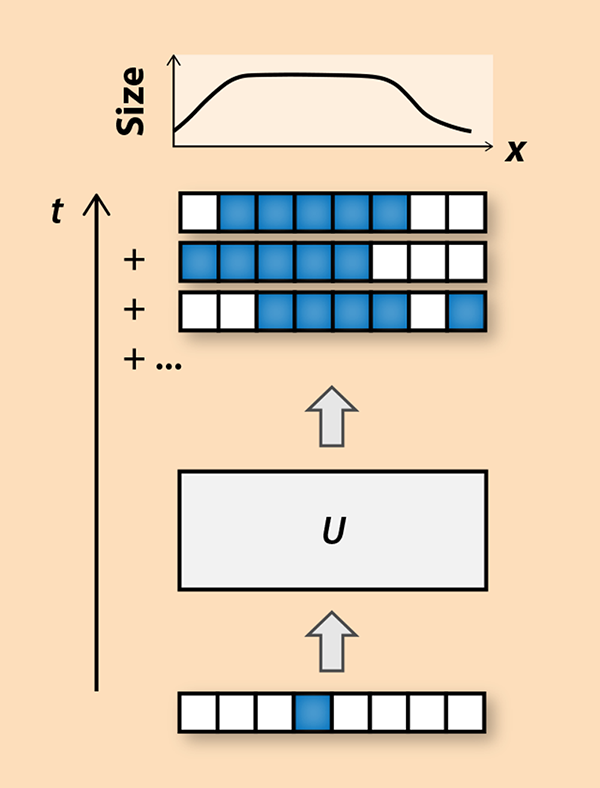
图2. 一个单翻转算符演化为拥有光滑波前的不同算符的连续叠加。
为了克服这种困难,Xu和Swingle转向了被称为布朗耦合簇(Brownian coupled cluster,BCC)模型,这些模型基于一种描述液体中原子不规则运动的布朗运动模型的量子版本。在BCC模型中,支配着这个系统动力学的哈密顿量不是一个常数,而是在各个时刻从一系列合适的哈密顿量中随机抽取的。笼统地说,这就像是在每轮牌局后洗牌一样,通过移除前几轮的记忆,这个牌局变得简单起来,因为玩家不需要记得前几轮发生过什么。研究人员们调整了BCC模型来为混沌信息置乱提供描述,在他们的数学推导中,这种记忆消除简化了系统动力学,这样混沌的传播可以用简单的微分方程来描述。
Xu和Swingle主要专注于一组描述随机、局部的自旋-自旋耦合的哈密顿量,通过这一组哈密顿量,他们分析了自由度为N的量子系统,并比较了N较大(N>>1)和N较小(N=2,对应一个传统量子比特)时的结果。为了简化分析过程,他们从无穷大的N入手并设定波前独立移动且不会改变形状。但是这个无穷大的N的界限是不稳定的,而且对于任意有限的N,他们发现波前会随着时间越来越平滑。通过更进一步的估算,他们开始着手解决更难解析的N较小的情况,并在波的传播和耗散中发现了相似的特征。
他们二人将他们的随机哈密顿方法得出的结果与那些用只通过数值计算的特定的哈密顿量(无随机性)得出的结果进行了比对,比较显示两者的性质一致,由此印证了BCC方法的有效性。但是需要特别指出,布朗模型和无随机性的哈密顿模型之间有本质不同:在后者中,系统的能量不守恒。他们也表明未来的研究也许会发展可以在遵守能量守恒的情况下量化描述量子混沌的机制。
对于量子混沌更加量化的描述和系统的理解如此重要有许多原因,其中一个与基础研究有关。近些年,在全息对偶(holographic duality)方面的进展引出了一种看法,这种看法认为引力也许是由量子混沌系统中的多体相互作用所产生的一种现象。例如,理论学家指出,一个落入黑洞的物体会在黑洞的事件视界上造成一种类似于混沌波前传播的扰动。通过帮助建立量子混沌的模型,新的算符置乱方法也许可以为解锁量子引力的秘密作出贡献。
这篇文章发表于Physical Review X。
作者:Xiaoliang Qi
翻译:宁文梦
审校:戴晨
引进来源:斯坦福大学理论物理研究所
















 京公网安备11010502039775号
京公网安备11010502039775号





